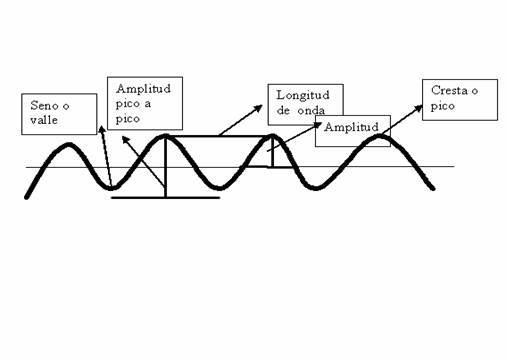
EL SONIDO: Es un movimiento ondulatorio que requiere indispensablemente de un medio para propagarse. El sonido no se propaga en el vacío, para que se transmita debe haber vibración molecular.
VELOCIDAD DEL SONIDO. La velocidad del sonido depende del medio donde se esté propagando, principalmente de su densidad, elasticidad y temperatura. En los sólidos la velocidad del sonido es mayor que en los líquidos y que en los gases.
VELOCIDAD DEL SONIDO EN EL AIRE. En el aire la velocidad del sonido varía de acuerdo a los cambios de temperatura a razón de 0.6 m/s por cada grado centígrado. A 00C la velocidad del sonido es de 331.7 m/s.
Para calcular la velocidad del sonido en el aire a cualquier temperatura se emplea la siguiente expresión:
VT = Vo + (0.6 m/s)T / 0C
Vo = 331.7 m/s
Ejemplo. Calcular la velocidad del sonido en el aire a una temperatura de 150C .
VT = Vo + (0.6 m/s)T / 0C
VT = 331.7 m/s + (0.6 m/s) (15 0C ) /0C
VT = 331.7 m/s + 9 m/s = 340.7 m/s
La velocidad del sonido en el aire a 150C es de 340.7 m/s.
La velocidad normal del sonido en el aire se toma igual a 340 m/s.
En el agua dulce = 1440 m/s
En agua salada = 1500 m/s.
En el hierro = 5100 m/s
En el vidrio = 5000 – 6000 m/s.
Ejercicios.
1. Calcular el tiempo que gasta el sonido en recorrer 1.5 Km .
a. En el aire a 200C .
b. En el agua
2. Un barco emite simultáneamente un sonido dentro del agua y otro en el aire. Si otro barco detecta los sonidos con una diferencia de 3 s., ¿A qué distancia están los barcos?
CUALIDADES DEL SONIDO
Los sonidos se caracterizan por tres cualidades muy particulares: la intensidad, el tono y el timbre. Es por ellas que diferenciamos un sonido de otro.
LA INTENSIDAD
Cualidad que nos permite percibir un sonido con mayor o menor energía. Se define como la potencia por unidad de área. I = P / A.
La intensidad sonora es:
a. Directamente proporcional a la masa vibrante.
b. Directamente proporcional al cuadrado de la amplitud del movimiento ondulatorio.
c. Inversamente proporcional al cuadrado de la distancia de la fuente sonora.
d. Directamente proporcional a la presión atmosférica.
NIVEL DE INTENSIDAD ( B )
El oído humano oye intensidades sonoras comprendidas entre un rango de 10-16 watts/cm2 hasta los 10- 4 watts/cm2. Este rango es bastante amplio de 1012 watts/cm2 , debido a este gran intervalo se utiliza una escala logarítmica en lugar de la escala natural ya que si la intensidad aumenta 10 veces el nivel aumenta 1 vez, si aumenta 100 veces el nivel aumenta 2, 1000 aumenta el nivel 3,....
El nivel de intensidad se mide en Bells o en decibelios = db.
B = 10 log I / Io db
Io =10-16 watts/cm2 = 10-12 watts/m2 = límite mínimo de audibilidad que corresponde a 0 db.
La intensidad máxima de 10-4 watts/cm2 = 1watt/m2 corresponde a un nivel de intensidad de 120 db.
NIVEL DE INTENSIDAD DE ALGUNOS SONIDOS.
Origen Nivel de I en db.
Umbral de la sensación sonora 0
Conversación en voz baja 20
Motor pequeño 40
Motocicleta 60
Conversación normal 65
Calle con mucho tráfico 80
Concierto de rock 120
Cerca de un avión a reacción 150
EL TONO
Es la cualidad del sonido que depende de la frecuencia. A frecuencias elevadas corresponden tonos altos o agudos, a frecuencias bajas corresponden tonos bajos o graves.
El oído humano es sensible a frecuencias comprendidas entre 20 Hz y 20000 Hz. Por debajo de este límite están los infrasonidos, ondas producidas por un sismo no son audibles por el oído humano y por encima los ultrasonidos. Algunos animales como pequeños roedores, perros, murciélagos, zorros, delfines, etc. sobrepasan estos límites de audibilidad.
Los ultrasonidos u ondas ultrasónicas tienen múltiples aplicaciones en medicina, minería, navegación aérea y marítima.
Por medio de ultrasonido, se detectan malformaciones congénitas en el feto y se pueden efectuar operaciones dentro del mismo vientre de la madre.
La voz del hombre tiene una frecuencia de 120 Hz, mientras la frecuencia de la voz femenina es de unos 240 Hz.
Las sirenas son aparatos que producen sonidos especiales según su configuración, y tienen que ver mucho con esta cualidad del sonido.
El tono de una sirena de disco, está dado por la siguiente ecuación;
N = n.w / 2p = nf
N = n.w / 2p = nf
N = Tono, o frecuencia del sonido a encontrar.
n = número de perforaciones del disco.
W = velocidad angular del disco
Ejercicio. Una sirena de 30 orificios emite un sonido cuya frecuencia es de 900 Vib/seg. ¿Calcular la frecuencia de la sirena?.
Una sirena de 50 orificios, a qué velocidad angular debe girar para producir un sonido de 500 Hz.
EL TIMBRE
Dos sonidos de la misma intensidad e igual tono pueden dar sensaciones muy diferentes. El timbre nos permite diferenciar una fuente sonora de otra, es decir, un sonido de otro.
Los sonidos puros son representados por gráficas sinusoidales.
Los instrumentos sonoros corresponden a los instrumentos musicales de cuerda, viento y percusión. En física se conocen como cuerdas, tubos, placas, láminas y varillas.
CUERDAS SONORAS.
Son dispositivos generalmente cilíndricos, fijos en sus extremos que al ser pulsados emiten sonidos.
La velocidad con que se propaga una onda sonora en una cuerda depende de la tensión y de la masa por unidad de longitud.
v = ÖT/ m m = m / L
1. La f de vibración de una cuerda es inversamente proporcional a la longitud.
2. La f de vibración de una cuerda es inversamente proporcional al diámetro.
3. La f de vibración de una cuerda es directamente proporcional a la raíz cuadrada de la tensión
4. La f de vibración de una cuerda es inversamente proporcional a la raíz cuadrada de la masa por unidad de longitud.
1. f1 / f2 = L2 / L1 2. f1 / f2 = D2 / D1
3. f1 / f2 = ÖT 1 / ÖT2 4. f1 / f2 = Öm 2 / Öm1
En el siglo pasado, el Francés Fourier demostró que cualquier función periódica de frecuencia f, puede expresarse como una suma de funciones sinusoidales de frecuencia f, 2f , 3f ,..................... llamadas frecuencia fundamental y armónicos.
ARMONICOS. Un armónico es un sonido cuya frecuencia es un múltiplo entero de otro llamado fundamental.
La frecuencia de cualquier armónico se encuentra por medio de la expresión:
fn = nv / 2L v = Ö(T/ m) m = m / L
n = número del armónico
L = longitud de la cuerda
m = masa de la cuerda
m = masa por unidad de longitud
v = velocidad del sonido en la cuerda
TUBOS SONOROS.
Son recipientes de forma cilíndrica, o prismática de madera, metal o de vidrio que limitan una columna de aire la cual produce un sonido cuando se hace vibrar.
Los tubos sonoros se clasifican en abiertos y cerrados.
Un tubo es abierto si el extremo distinto a la embocadura es abierto, en caso contrario es cerrado.
Para tubos abiertos: fn = nV/2L
Para tubos cerrados: fn = nV/4L , para n impar
EFECTO DOPPLER
El efecto Doppler consiste en un cambio de la frecuencia que percibe un receptor con respecto a una fuente sonora. Este cambio es debido a la relatividad del movimiento de la fuente sonora y del receptor.
Cuando hay acercamiento la frecuencia percibida por el observador aumenta, en caso contrario disminuye.
El Efecto Doppler, está regido por la siguiente ecuación:
fo = f (V ± Vo / V + Vf )
Se toma + / - Cuando se acercan.
Se toma - / + cuando se alejan.
fo = Frecuencia percibida por el receptor
f = Frecuencia emitida por la fuente
V = Velocidad del sonido en el aire = 340 m/s
Vo = Velocidad del observador
Vf = Velocidad de la fuente
EL ECO.
Fenómeno producido por la reflexión del sonido sobre una superficie grande, de modo que el oyente percibe dos sonidos: El original o incidente y el reflejado o eco.
Para que se produzca el eco es indispensable que la fuente sonora que emite el sonido original esté situada a por lo menos 17m del obstáculo reflector. La distancia mínima para que haya eco se debe a que en el oyente la sensación sonora persiste durante 0,1 seg., tiempo que debe transcurrir entre el sonido original y el reflejado para que no haya interferencia.
La velocidad normal del sonido es de 340 m/s.
e = vt ®340 m/s (0,1 s) = 34m. La distancia de 34 m corresponde a la ida y venida del sonido, por lo tanto 34m/2=17m
Llámase resonancia acústica a la reproducción de un sonido por un resonador.
Para que haya resonancia es necesario que los dos resonadores estén al unísono, es decir, que tengan la misma frecuencia.
Actualmente se habla de resonancia magnética, aplicación fundamental en medicina.
EJERCICIOS SOBRE ACUSTICA.
1. Hallar la velocidad del sonido en el aire, a una temperatura de 320C .
2. Un sonido se propaga en el aire a razón de 345 m/s. ¿Qué temperatura tiene el medio?.
3. Calcular en db el nivel de intensidad de un sonido, cuya intensidad es de 1.5 x 10-6 vatios/cm2 ,
4. El nivel de intensidad de un sonido es de 62.56 db. ¿A qué intensidad en vatios/cm2 equivale?
5. La intensidad de un sonido es el doble de la mínima intensidad audible por el hombre. ¿Cuál es el nivel de intensidad?
6. Una cuerda tiene una masa por unidad de longitud de 0.5 gr/cm. Una longitud de 75 cm y está sometida a una tensión de 5N. ¿Cuál es la frecuencia del sonido fundamental que emite?.
7. Una cuerda sometida a una tensión de 50N, vibra con una frecuencia de 80 Hz. ¿Cuál es la nueva frecuencia si la tensión de la cuerda se aumenta en un 20%?
8. ¿Cuál debe ser la longitud de un tubo abierto para que su sonido fundamental tenga una frecuencia de 75S-1?
9. Una fuente sonora que emite un sonido de 360 Hz, se acerca a 80Km/h hacia un observador que se encuentra en reposo. ¿ Cuál es la frecuencia detectada por el observador?.
10. Un autobús viaja a una velocidad de 16.6 m/s, y su corneta emite un sonido cuya frecuencia es de 280 Hz. Si una persona camina en diferente sentido a una velocidad de 3 m/s. ¿Qué frecuencia percibe la persona?.
11. Una persona percibe que la frecuencia del sonido emitido por un tren es 350 Hz cuando se acerca y de 315 Hz cuando se aleja. ¿ Cuál es la velocidad del tren?.
12. Una cuerda de piano tiene una longitud de 40 cm y una masa de 5 gr y se halla tensionada 2N ¿Cuál será el valor de su frecuencia en su tercer armónico?.
13. Una cuerda de violín de 30 cm vibra con una frecuencia fundamental de 540 Hz. Se inmoviliza uno de sus puntos con el dedo de tal forma que la longitud es ahora de 25 cm . ¿Cuál es la nueva frecuencia fundamental de esta cuerda?.
14. Una cuerda de 99 cm de longitud y 22 g de masa, se somete a una tensión de 5 N. Si se producen 30 vibraciones en 10 segundos, calcula:
a. La frecuencia de la onda generada.
b. El periodo de vibración.
c. La velocidad de propagación de la onda.
d. La longitud de onda.
e. Qué cambio experimenta la velocidad de propagación de la onda si la frecuencia aumenta?.
f. Cómo se relaciona la longitud de onda con la frecuencia?
g. Qué pasa con la longitud de onda si la frecuencia aumenta?.