MOVIMIENTO ONDULATORIO

MOVIMIENTO ONDULATORIO

Una señal es un cambio que se produce en un medio. Son ejemplos de señales: el cambio de un semáforo, el pitazo de un arbitro,  el sonido de una sirena, el movimiento de una mano, guiñar un ojo,...

Una señal se puede transmitir de un lugar a otro por medio de uno o de varios portadores.

Cuando sólo hay un portador en llevar la señal se dice que hay comportamiento corpuscular.

Cuando hay varios portadores se habla de comportamiento ondulatorio.


http://www.youtube.com/watch?v=jzQSJsjtrAk&feature=related

CLASES DE ONDAS

En este curso se  estudiarán las ondas mecánicas. Una onda mecánica es una perturbación que se transmite en un medio en forma sucesiva y gradual. Las ondas son portadoras de energía y no de materia.

Otro tipo importante de ondas son las electromagnéticas que se pueden transmitir hasta en el vacío y a la velocidad de la luz. Por ejemplo las ondas de radio y T.V.

Las ondas mecánicas se dividen en tres tipos:

Ondas Transversales Hacen que las partículas del medio oscilen perpendicularmente  a la dirección de propagación de la onda. Ondas en un resorte o en una cuerda.

Ondas Longitudinales. Hacen que las partículas del medio se muevan paralelamente a la dirección de propagación de la onda. El sonido.

Ondas Superficiales. Se toman como la combinación de las dos anteriores.

Algunas ondas son detectadas fácilmente, otras por el contrario necesitan de aparatos especiales para  detectarlas y estudiarlas. Los osciloscopios  son aparatos que detectan este tipo de ondas.

Matemáticamente una onda se representa por una gráfica sinuosoidal

[ Y = A Sen ( x + c ) ]

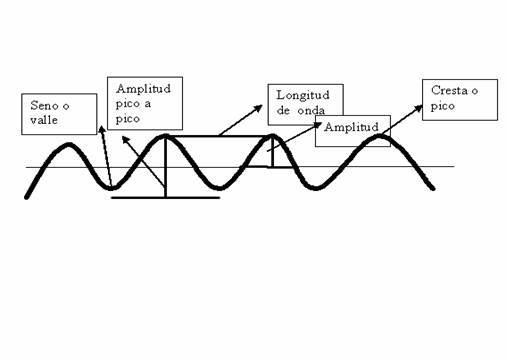
Son elementos de una onda: La longitud ( l ), nodos, crestas y valles (antinodos), la amplitud.

REPRESENTACIÓN DE UNA SEÑAL.

Longitud de Onda ( l ):  Es la distancia más corta para que el patrón ondulatorio entre puntos se repita.

Elongación (Y): Cualquier separación con respecto a la posición de equilibrio.

Amplitud (A): Es la máxima separación de la onda con respecto a su posición de equilibrio (x).

Crestas ( C ): Partes más elevadas.

Valles ( V ): Partes más bajas.

Nodos ( N ): Cortes de la onda con el eje  x.

Antinodos: Conjunto de crestas y valles.

Periodo( T ): Tiempo para recorrer una longitud de onda.

Frecuencia (f) : Número de vibraciones por segundo. Su unidad  es el Hz = vib/seg.  KHz = 1000 Hz  MHz = 1000 000 Hz.

Siendo ( l ):la distancia, f  la frecuencia y v la  velocidad de la onda, entonces:

Velocidad = (longitud) (frecuencia)

  v = l.. f     ó      v =  l /T

Ejercicios.

La longitud de onda de un movimiento ondulatorio es de 50 cm y su  frecuencia es de 10 Hz. ¿Cuál es la velocidad del movimiento?.

Calcular la longitud de onda del sonido producido por una guitarra cuya frecuencia es de 440 Hz, siendo la velocidad del sonido en el aire de 340 m/seg.?

Una onda de radio, tiene  una frecuencia de 99.5 MHz. ¿Cuál es su longitud de onda?.

Una onda sonora con una frecuencia de 265 Hz posee una longitud de onda de 1.29 m. ¿Cuál es la velocidad de dicha onda?

Una onda sonora tiene una frecuencia de 262 Hz. ¿Cuál es el tiempo que transcurre entre dos crestas sucesivas?.

Se escucha en una estación de radio: H.J.D.X en 1070 Khz (ondas largas). L.Q.X.R en 6120 Khz (ondas cortas). ¿Cuál es el valor de la longitud de onda de dicha emisora?

C = 3x10⁵ Km/seg.

FUNCIÓN DE ONDA

La función de onda permite describir la forma de una onda en cualquier instante. Esta función depende de la posición de cada punto, del medio de propagación y  del tiempo de iniciada la perturbación.

La función   y = f(x,t).

Entre el instante t = 0 y el instante t, la onda se desplaza una distancia d = vt

Para el instante t=0, le corresponde la función de onda

y = A sen wt, osea:

 Tomando La ecuación  queda   y = A sen (kx)

Si la onda se propaga  con una velocidad v, en el instante t, la onda se ha desplazado una distancia d hacia la derecha a lo largo del eje x, tal que d = v.t.

La función de onda en un instante t es:

               y = A sen [k (x-v.t)]

Como v = l / T, tenemos que, v / l = 1/ T, además,  

w = 2p / T

Quedando la función de onda como:

y(x,t) = A sen [kx – wt)  cuando se propaga hacía la derecha.

y(x,t) = A sen [kx + wt)  cuando se propaga hacía la izquierda.

El ángulo (kx + wt) se llama ángulo de fase.

Indistintamente se puede expresar la ecuación con la función seno o con la función coseno.

Otras formas de escribirse la función de onda son:

y(x,t) = A sen w ( t – x/v)

y(x,t) = A sen 2p(t/T – x/l)

“La función y(x,t), corresponde a la posición vertical de la partícula (elongación), situada a una distancia x del foco, en el instante t.”

Ejercicio 1.

En el extremo izquierdo de una cuerda, se produce un MAS en dirección de la cuerda con una amplitud de  0.02m y una frecuencia de 8 Hz. La onda se propaga a una velocidad de 20 m/s, calcular:

a)     la amplitud.

b)    la frecuencia

c)     el periodo

d)    la longitud de onda

e)     la ecuación de la onda

Ejercicio 2.

La  ecuación de una onda armónica es:

y = 0.1 cos ( 4x + 2t ), con x y y expresados en metros y t en segundos.

Determina:

a)     la amplitud

b)    la longitud de onda

c)     el periodo de vibración

d)    la frecuencia

e)     la velocidad de propagación

f)     la posición de un punto del medio para el cual x = 0.5m en t = 2s.

Ejercicio 3.

A partir de la siguiente función de onda en la cual x y y se expresan en centímetros y t en segundos,

y = 3 cos (4px+ 100pt) calcula:

a)     la amplitud de la onda

b)    la longitud de onda.

c)     la frecuencia

d)    la velocidad de propagación

PROPIEDADES O CARACTERISTICAS DE LAS ONDAS.

Las ondas al propagarse presentan  varios fenómenos:

1. PRINCIPIO DE HUYGENS

 Todo punto de un medio, a donde llega un movimiento ondulatorio de un centro primario principal, este se convierte en un nuevo centro emisor de ondas.

2. REFLEXION

                                           

Una onda al chocar con un obstáculo, se refleja.

OP = Onda incidente

PQ = Onda  reflejada

i = Angulo de incidencia

r = Angulo reflejado

NP = normal

SS’ = Obstáculo

LEY FUNDAMENTAL: “El ángulo de incidencia es igual al ángulo de reflexión”.  <i = <r

3. REFRACCION. 

Es el cambio de velocidad que experimenta una onda al pasar de un medio a otro 

LEY  FUNDAMENTAL: “La razón entre el seno del ángulo de incidencia

y el seno del ángulo de refracción  es igual a la razón entre  las velocidades del movimiento ondulatorio en ambos medios”.

4.    INTERFERENCIA.

Cuando a un punto llegan simultáneamente dos o más ondas, la amplitud con que vibra este punto es la resultante de la suma algebraica de cada una de las ondas. También se llama  principio de superposición.

Un tipo de interferencia muy importante ocurre cuando dos ondas de la misma amplitud y frecuencia  se propagan en sentido contrario, en un mismo medio, estas ondas reciben el nombre de ONDAS ESTACIONARIAS

  5.    DIFRACCION

La onda pasa y rodea el obstáculo ó la abertura.      Cuando una onda pasa cerca de un obstáculo o a través de un orificio, se produce un cambio en la curvatura de la onda.

.

Para que haya difracción el obstáculo u orificio debe ser  menor que la longitud de la onda.

6.POLARIZACION. 

Fenómeno que se presenta en las ondas transversales, que consiste en reducir todos los planos de vibración  de la onda a uno solo.